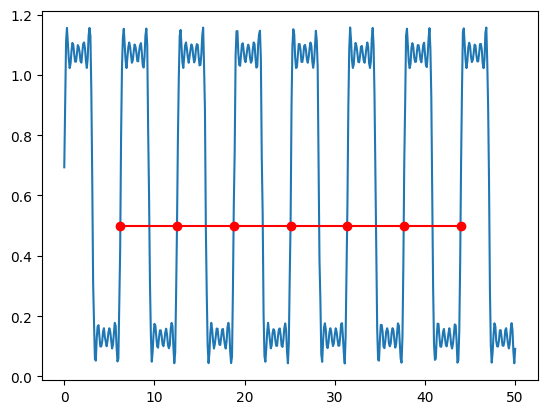
# from https://stackoverflow.com/questions/15112964/digitizing-an-analog-signal
from __future__ import division
import numpy as np
def find_transition_times(t, y, threshold):
"""
Given the input signal `y` with samples at times `t`,
find the times where `y` increases through the value `threshold`.
`t` and `y` must be 1-D numpy arrays.
Linear interpolation is used to estimate the time `t` between
samples at which the transitions occur.
"""
# Find where y crosses the threshold (increasing).
lower = y < threshold
higher = y >= threshold
transition_indices = np.where(lower[:-1] & higher[1:])[0]
# Linearly interpolate the time values where the transition occurs.
t0 = t[transition_indices]
t1 = t[transition_indices + 1]
y0 = y[transition_indices]
y1 = y[transition_indices + 1]
slope = (y1 - y0) / (t1 - t0)
transition_times = t0 + (threshold - y0) / slope
return transition_times
def periods(t, y, threshold):
"""
Given the input signal `y` with samples at times `t`,
find the time periods between the times at which the
signal `y` increases through the value `threshold`.
`t` and `y` must be 1-D numpy arrays.
"""
transition_times = find_transition_times(t, y, threshold)
deltas = np.diff(transition_times)
return deltas
if __name__ == "__main__":
import matplotlib.pyplot as plt
# Time samples
t = np.linspace(0, 50, 501)
# Use a noisy time to generate a noisy y.
tn = t + 0.05 * np.random.rand(t.size)
y = 0.6 * ( 1 + np.sin(tn) + (1./3) * np.sin(3*tn) + (1./5) * np.sin(5*tn) +
(1./7) * np.sin(7*tn) + (1./9) * np.sin(9*tn))
threshold = 0.5
deltas = periods(t, y, threshold)
print("Measured periods at threshold %g:" % threshold)
print(deltas)
print("Min: %.5g" % deltas.min())
print("Max: %.5g" % deltas.max())
print("Mean: %.5g" % deltas.mean())
print("Std dev: %.5g" % deltas.std())
trans_times = find_transition_times(t, y, threshold)
plt.plot(t, y)
plt.plot(trans_times, threshold * np.ones_like(trans_times), 'ro-')
plt.show()
# The output:
# Measured periods at threshold 0.5:
# [ 6.29283207 6.29118893 6.27425846 6.29580066 6.28310224 6.30335003]
# Min: 6.2743
# Max: 6.3034
# Mean: 6.2901
# Std dev: 0.0092793