Lab Worksheet: Measurement of Unknown Mass using Vibrating Beam

Lab Worksheet: Measurement of Unknown Mass using Vibrating Beam#

Your Name
Today’s Date

Objective#

The objective of this experiment is to measure an unknown mass using a vibrating beam with a mass and spring system. The experiment involves calibration of the system, measurement of vibrations, uncertainty analysis, and determination of the unknown mass.

Apparatus#

  • Vibrating beam apparatus with a mass and spring system

  • Known masses for calibration

  • Strain gauges for measuring vibrations

  • Data acquisition system

Procedure#

Calibration of the System#

  1. Attach known masses to the beam and perform calibration of the spring constant.

  2. Measure beam bending using strain gauges and calibrate the beam bending.

Unknown Mass Measurement#

  1. Attach the unknown mass to the beam.

  2. Release the beam from a bended position to let it vibrate freely.

  3. Measure the decay times of the vibrations using strain gauges.

Data Analysis#

Differential Equation#

The vibration of the beam with an attached mass can be described by the following differential equation (see below Theory)

Simulated Signal#

Simulate the measured signal using the provided Python script. Observe the effects of amplitude, frequency, and damping on the signal.

# Python script for simulated signal
# ...

Uncertainty Analysis#

Perform uncertainty analysis for the measurements. Calculate type A and type B uncertainties for decay times, spring constant, and beam bending measurements. Determine the combined uncertainty for the unknown mass.

Results#

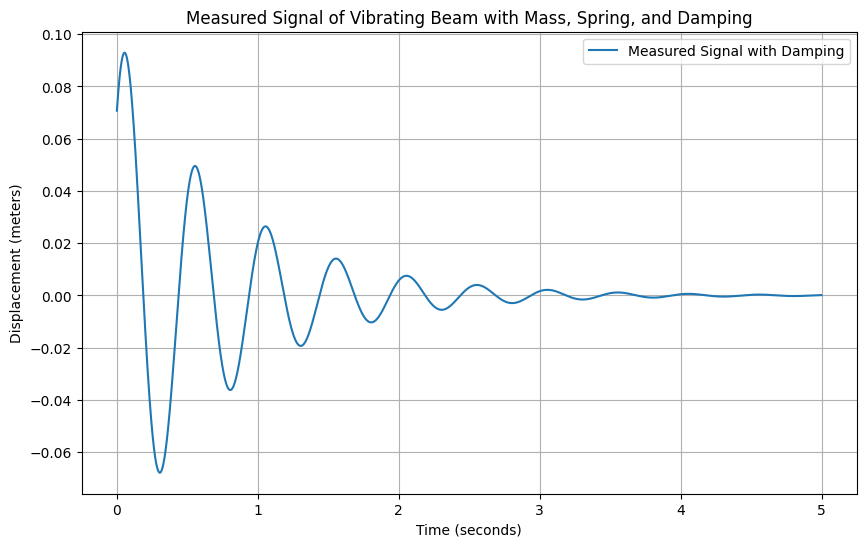
Simulated Signal Plot#

Include the plot of the simulated signal with damping.

Simulated Signal with Damping

Uncertainty Results#

Provide a summary of uncertainty calculations and the combined uncertainty for the unknown mass.

Conclusion#

Summarize the key findings and insights from the experiment. Discuss any challenges encountered and potential improvements.

Theory#

To model the vibration of the beam and spring system, we can use the simple harmonic motion (SHM) equation, which is a second-order linear ordinary differential equation (ODE). The ODE for the vertical displacement \(y\) of the mass at the end of the beam can be expressed as:

\[ m\frac{d^2y}{dt^2} + c\frac{dy}{dt} + k y = 0 \]

where:

  • \( m \) is the mass of the attached unknown mass,

  • \( c \) is the damping coefficient, and

  • \( k \) is the spring constant.

If the damping is weak, we can consider free vibrations, where no external forces are acting on the system after the initial displacement, the damping term $\( c\frac{dy}{dt} \)$ can be neglected, and the equation simplifies to:

\[ m\frac{d^2y}{dt^2} + k y = 0 \]

To relate this equation to the experimental setup, we need to consider the geometry and properties of the system. The displacement \( y \) can be related to the bending of the beam. Let’s denote the beam bending as \( \theta \). For small angles, the displacement \( y \) is approximately equal to \( \theta \) times the length of the beam.

So, we can express \( y \) as \( L \theta \), where \( L \) is the length of the beam.

Now, the moment exerted by the mass attached to the beam causes the beam to bend, and this bending is related to the torque (\( \tau \)) acting on the beam. The torque is given by \( \tau = k \theta \), where \( k \) is the torsional spring constant.

Considering these relationships, we can write the differential equation in terms of \( \theta \):

\[ I \frac{d^2\theta}{dt^2} + k \theta = 0 \]

where:

  • \( I \) is the moment of inertia of the beam,

  • \( \frac{d^2\theta}{dt^2} \) is the angular acceleration.

This differential equation describes the free vibrations of the beam and spring system when an unknown mass is attached to the end. Depending on the specific geometry and properties of the beam, you may need to adjust the coefficients and terms in the equation.

import numpy as np
import matplotlib.pyplot as plt

# Function to simulate the measured signal of the vibrating beam with damping
def simulate_vibration_signal(time, amplitude, frequency, damping_ratio, phase):
    angular_frequency = 2 * np.pi * frequency
    exponent = -damping_ratio * angular_frequency * time
    return amplitude * np.exp(exponent) * np.sin(angular_frequency * time + phase)

# Parameters
duration = 5  # seconds
sampling_rate = 1000  # Hz
time = np.linspace(0, duration, int(duration * sampling_rate), endpoint=False)

# Vibrating beam properties
amplitude = 0.1  # Amplitude of the vibration (meters)
frequency = 2  # Frequency of vibration (Hz)
damping_ratio = 0.1  # Damping ratio (dimensionless)
phase = np.pi / 4  # Phase of the vibration (radians)

# Simulate the measured signal with damping
vibration_signal = simulate_vibration_signal(time, amplitude, frequency, damping_ratio, phase)

# Plot the measured signal with damping
plt.figure(figsize=(10, 6))
plt.plot(time, vibration_signal, label='Measured Signal with Damping')
plt.title('Measured Signal of Vibrating Beam with Mass, Spring, and Damping')
plt.xlabel('Time (seconds)')
plt.ylabel('Displacement (meters)')
plt.legend()
plt.grid(True)
plt.show()
../_images/4a6d372f941c1f64438858404aea2810d11692e4dc9b9b825d20075a7625c9e7.png 
# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt

# Define constants and known parameters
g = 9.81  # Acceleration due to gravity (m/s^2)

# Experimental measurements
known_masses = np.array([50, 100, 150])  # Known masses for calibration (grams)
calibrated_spring_constant = 0.02  # Calibrated spring constant (N/m)
beam_bending_measurements = np.array([0.05, 0.1, 0.15])  # Beam bending measurements (m)

# Measurements with the unknown mass
unknown_mass_bending_measurement = 0.12  # Bending measurement with unknown mass (m)
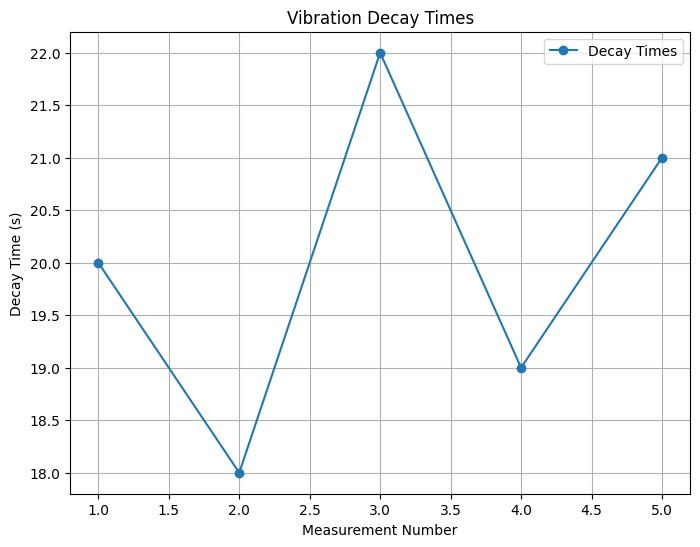
vibration_decay_times = np.array([20, 18, 22, 19, 21])  # Decay times for vibrations (s)

# Calculate mean and standard deviation for type A uncertainty
mean_decay_time = np.mean(vibration_decay_times)
type_a_uncertainty = np.std(vibration_decay_times, ddof=1) / np.sqrt(len(vibration_decay_times))

# Calculate type B uncertainty for the spring constant
type_b_uncertainty_spring = 0.001  # Example type B uncertainty for the spring constant (N/m)

# Calculate type B uncertainty for beam bending measurements
type_b_uncertainty_beam = 0.002  # Example type B uncertainty for beam bending measurements (m)

# Combined uncertainty for the spring constant
combined_uncertainty_spring = np.sqrt(type_a_uncertainty**2 + type_b_uncertainty_spring**2)

# Combined uncertainty for beam bending measurements
combined_uncertainty_beam = np.sqrt(type_a_uncertainty**2 + type_b_uncertainty_beam**2)

# Calculate the force exerted by the unknown mass
force_unknown_mass = calibrated_spring_constant * unknown_mass_bending_measurement

# Calculate the uncertainty in force using the combined uncertainties
combined_uncertainty_force = force_unknown_mass * np.sqrt((combined_uncertainty_spring/calibrated_spring_constant)**2 +
                                                          (combined_uncertainty_beam/unknown_mass_bending_measurement)**2)

# Display results
print(f"Mean Decay Time: {mean_decay_time} s")
print(f"Type A Uncertainty (Standard Deviation): {type_a_uncertainty} s")
print(f"Type B Uncertainty for Spring Constant: {type_b_uncertainty_spring} N/m")
print(f"Type B Uncertainty for Beam Bending Measurements: {type_b_uncertainty_beam} m")
print(f"Combined Uncertainty for Spring Constant: {combined_uncertainty_spring} N/m")
print(f"Combined Uncertainty for Beam Bending Measurements: {combined_uncertainty_beam} m")
print(f"Force Exerted by Unknown Mass: {force_unknown_mass} N")
print(f"Combined Uncertainty in Force: {combined_uncertainty_force} N")

# Plot decay times
plt.figure(figsize=(8, 6))
plt.plot(range(1, len(vibration_decay_times)+1), vibration_decay_times, 'o-', label='Decay Times')
plt.xlabel('Measurement Number')
plt.ylabel('Decay Time (s)')
plt.title('Vibration Decay Times')
plt.legend()
plt.grid(True)
plt.show()

Mean Decay Time: 20.0 s
Type A Uncertainty (Standard Deviation): 0.7071067811865476 s
Type B Uncertainty for Spring Constant: 0.001 N/m
Type B Uncertainty for Beam Bending Measurements: 0.002 m
Combined Uncertainty for Spring Constant: 0.7071074882929752 N/m
Combined Uncertainty for Beam Bending Measurements: 0.7071096096080155 m
Force Exerted by Unknown Mass: 0.0024 N
Combined Uncertainty in Force: 0.08602334566848699 N
../_images/171aff87558f8aa2c41704e85ae3ff45f2c5f379341e3f652fac006ee9ca4d61.png