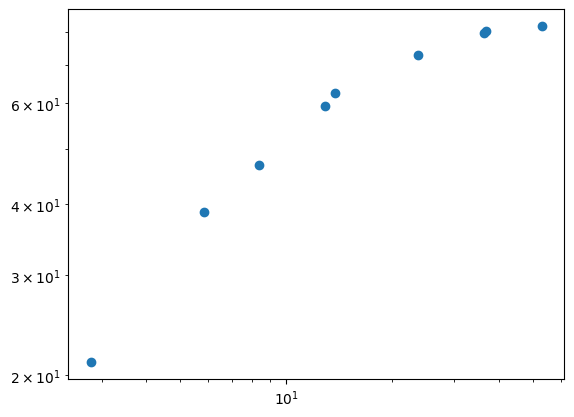
Calibration of non-linear (logarithmic) function

Calibration of non-linear (logarithmic) function#

from pylab import *
%pylab inline
from io import StringIO

%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib

/home/user/Documents/GitHub/mechanical-engineering-metrology-and-measurements/.venv/lib/python3.12/site-packages/IPython/core/magics/pylab.py:166: UserWarning: pylab import has clobbered these variables: ['diagonal', 'matrix_transpose', 'trace', 'bool', 'outer', 'tensordot', 'vecdot', 'min', 'pow', 'matmul', 'abs', 'cross', 'fft', 'random', 'round', 'max', 'power']
`%matplotlib` prevents importing * from pylab and numpy
  warn("pylab import has clobbered these variables: %s"  % clobbered +

# create two signals: concentration and temperature
c = StringIO("""
1.095406121 3.887032952 6.956500526 9.486921797 \
13.96944459 14.86018043 23.19810833 24.53008787 \
24.72311112 37.44113657 38.05523491 54.1881169""")


T = StringIO("""91.72763561 70.60278306 \
53.0039356 45.03419592 32.45847839 29.03763728 13.49252686 \
12.0641877 18.91647307 12.01351046 11.49379565 9.671537342 """)

c = loadtxt(c)
T = loadtxt(T)

plot(c,T,'o')

[<matplotlib.lines.Line2D at 0x72cbee451370>]
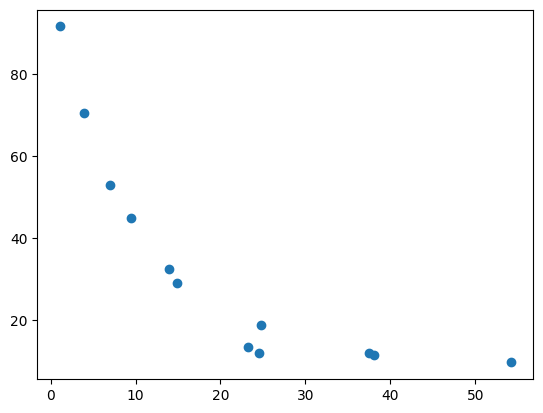
../_images/f1ed08e2f7faacc3f559f9bb32d9a33937e8b75d3977a54145682e8faef4fcf3.png 
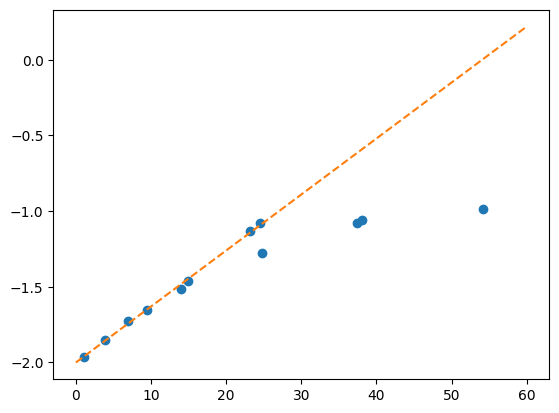
a = -np.log10(T)
plot(c,a,'o')

[<matplotlib.lines.Line2D at 0x72cbee497380>]
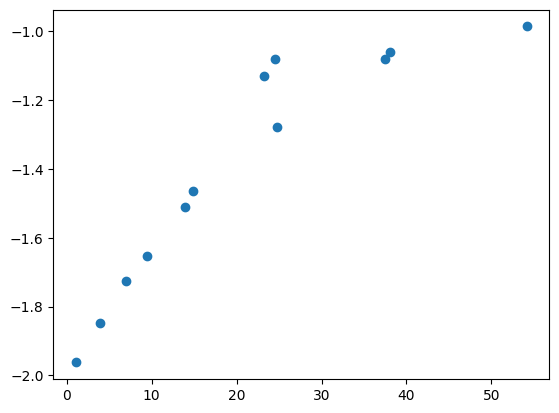
../_images/0e5aab64092bcacf6fbf027fc0f2ce3c9813b0405f58e39a7225353ac91d6990.png

see the linear part and the “saturated part”, use only the linear one#

ind = c < 24
plot(c[ind],a[ind],':o')

[<matplotlib.lines.Line2D at 0x72cbee1a1f70>]
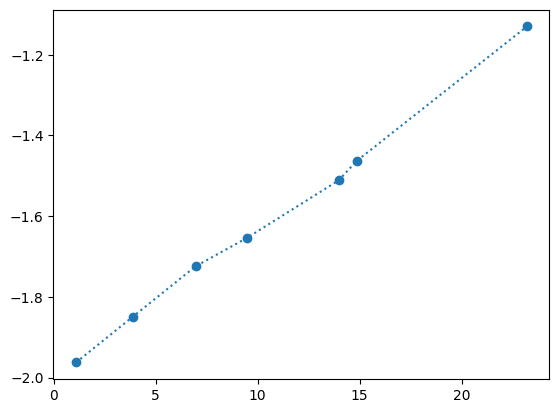
../_images/26ec34e35c4392d3b96a2d5ea06cec1875e0b3ace2fcc21a7bf7717852a6519b.png 
polyfit(c[ind],a[ind],1)

array([ 0.03674248, -1.99891754])

plot(c,a,'o')
c1 = linspace(0,60,100)
a1 = 0.037*c1-2.0
plot(c1,a1,'--')

[<matplotlib.lines.Line2D at 0x72cbee231df0>]
../_images/8978f4efcf6c33a56933d768332956e8dda30cbf37f44ecb8dd0153df130e57a.png 
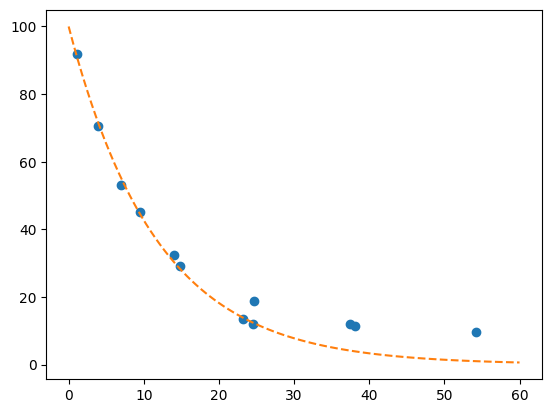
plot(c,T,'o')
a1 = 0.037*c1-2.0
plot(c1,10**(-a1),'--')

[<matplotlib.lines.Line2D at 0x72cbee297ef0>]
../_images/7f2f0fb2e1fe6114292dca227336413b2602e1cf5e54dc276b83953cb43223ee.png 
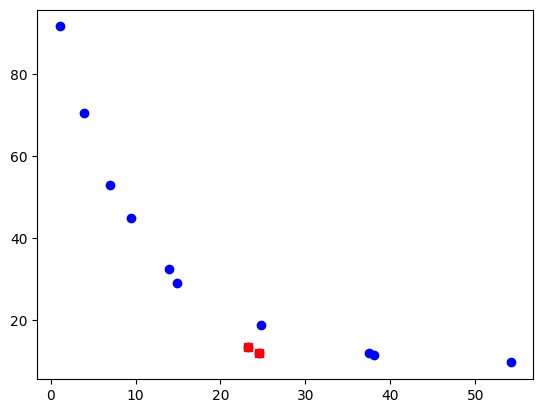
print(f'c = {c}')
print(f'T = {T}')

c = [ 1.09540612  3.88703295  6.95650053  9.4869218  13.96944459 14.86018043
 23.19810833 24.53008787 24.72311112 37.44113657 38.05523491 54.1881169 ]
T = [91.72763561 70.60278306 53.0039356  45.03419592 32.45847839 29.03763728
 13.49252686 12.0641877  18.91647307 12.01351046 11.49379565  9.67153734]

plot(c,T,'bo',c[6:8],T[6:8],'rs')

[<matplotlib.lines.Line2D at 0x72cbee488c20>,
 <matplotlib.lines.Line2D at 0x72cbee30d490>]
../_images/5e3901b2d37942207d4526ffcae1e38527220d052eea11ea4e728e69677c9b27.png 
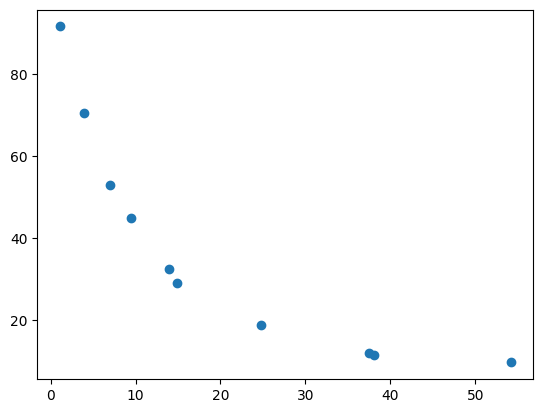
c2 = c.copy()
T2 = T.copy()
mask = ones(c2.shape[0],dtype=bool)
mask[[6,7]] = False
plot(c2[mask],T2[mask],'o')

[<matplotlib.lines.Line2D at 0x72cbebf45d90>]
../_images/3969e2c8ed8ad8ebc3a3cb478f37d395efdbf0e765eb1a2687c1e81d9bdeb9a8.png 
plot(c2[mask]-c2[0],T2[mask]-T2[0],'o')

[<matplotlib.lines.Line2D at 0x72cbebf871d0>]
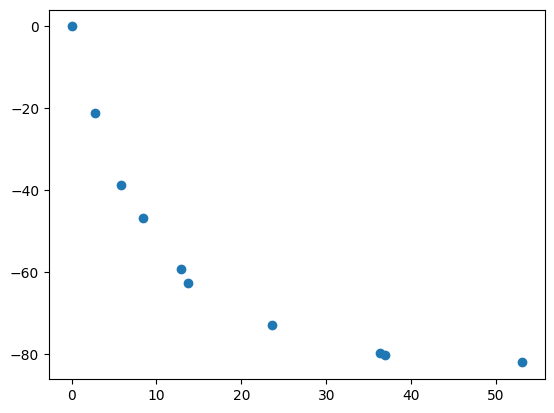
../_images/689720781e99a51eac86a6b8c2e00f913636b93cb2b622fac8f7e0073f0e48dc.png 
c3 = c2[mask] - c2[0]
T3 = T2[0] - T2[mask]

c3

array([ 0.        ,  2.79162683,  5.86109441,  8.39151568, 12.87403847,
       13.76477431, 23.627705  , 36.34573045, 36.95982879, 53.09271078])

loglog(c3,T3,'o')

[<matplotlib.lines.Line2D at 0x72cbebe05bb0>]
../_images/f6345ca3b0fab124273cbe5a0029509f252eb072a188709506fee3a88fc275e8.png
Contents