Fourier transforms

From very naive approximations of the spectrum to more complex examples:

from scipy import fft
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

Two basic ploting functions that repeat the actuall spectral analysis:

import sys
sys.path.append('../scripts')
from signal_processing import *

More elaborate example, demonstration of a leakage effect:

# We sample a signal at fs = 200 Hz and record 256 points"

# true values
A = 1.0 # Volt, amplitude
ff = 10.0 # Hz, signal frequency, zero harmonics


# We will work with different sampling frequencies
# and different lengths of records:

fs = 200.0 #Hz
N = 256 # points

plotSignal(A,ff,fs,N)

---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
Cell In[3], line 14
     11 fs = 200.0 #Hz
     12 N = 256 # points
---> 14 plotSignal(A,ff,fs,N)

File ~/Documents/repos/engineering_experiments_measurements_course/book/signal_processing/../scripts/signal_processing.py:47, in plotSignal(A, ff, fs, N)
     45 t = np.arange(0.0, T, T/N)  # sampling time steps
     46 y = A*np.sin(2*np.pi*ff*t)  # sampled signal
---> 47 frq, Y = spectrum(y, fs)  # FFT(sampled signal)
     49 # Plot
     50 fig, ax = plt.subplots(2, 1, figsize=(10, 8))

File ~/Documents/repos/engineering_experiments_measurements_course/book/signal_processing/../scripts/signal_processing.py:36, in spectrum(y, Fs)
     34 T = n/Fs
     35 frq = k/T  # two sides frequency range
---> 36 frq = frq[range(np.int(n/2))]  # one side frequency range
     37 Y = 2*fft.fft(y)/n  # fft computing and normalization
     38 Y = Y[range(np.int(n/2))]

File ~/Documents/repos/engineering_experiments_measurements_course/.conda/lib/python3.12/site-packages/numpy/__init__.py:397, in __getattr__(attr)
    392     warnings.warn(
    393         f"In the future `np.{attr}` will be defined as the "
    394         "corresponding NumPy scalar.", FutureWarning, stacklevel=2)
    396 if attr in __former_attrs__:
--> 397     raise AttributeError(__former_attrs__[attr], name=None)
    399 if attr in __expired_attributes__:
    400     raise AttributeError(
    401         f"`np.{attr}` was removed in the NumPy 2.0 release. "
    402         f"{__expired_attributes__[attr]}",
    403         name=None
    404     )

AttributeError: module 'numpy' has no attribute 'int'.
`np.int` was a deprecated alias for the builtin `int`. To avoid this error in existing code, use `int` by itself. Doing this will not modify any behavior and is safe. When replacing `np.int`, you may wish to use e.g. `np.int64` or `np.int32` to specify the precision. If you wish to review your current use, check the release note link for additional information.
The aliases was originally deprecated in NumPy 1.20; for more details and guidance see the original release note at:
    https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations

Note:

1. leakage at around 10 Hz

2. peak is below 1 Volt

3. we can get the spectrum up to half of sampling frequency

4. frequency resolution is \(\Delta f = 1/T = 0.781\) Hz

Let us try to minimize the leakage:

Let’s first increase the sampling rate, stay with N = 256

fs = 1000.0 #Hz
N = 512 # points
plotSignal(A,ff,fs,N)

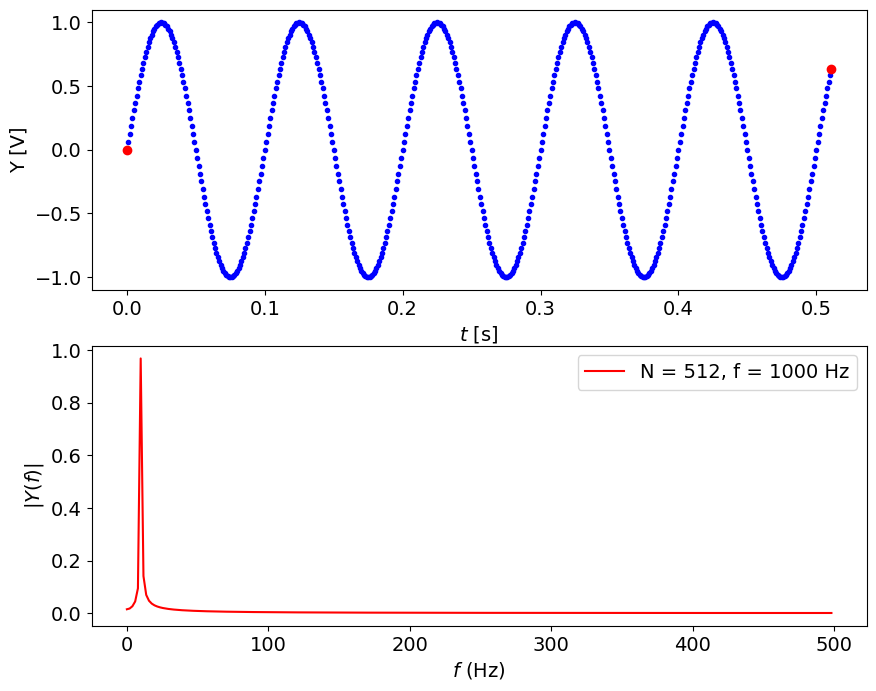
Note:

1. resolution in time is great BUT:

2. resolution in frequency is worse, \(\Delta f = 1/T = 1/0.25 = 3.91\) Hz

3. we see up to 500 Hz, but have here only 128 useful points

4. leakage is severe, the peak amplitude is about 0.66 Volt

5. peak location is now 11.7 Hz

MORE IS NOT NECESSARILY BETTER

###Let us try to minimize the leakage problem sampling closer to the Nyquist frequency

fs = 25.0 #Hz
N = 256 # points
plotSignal(A,ff,fs,N)

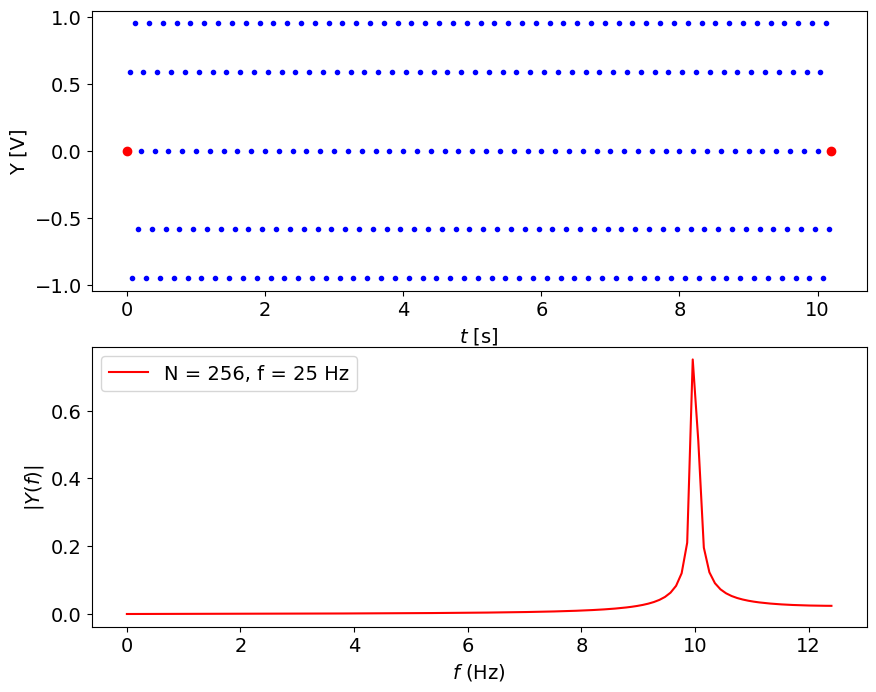
Note:

1. sine does not seem to be a sine wave, time resolution is bad for Nyquist frequency

2. frequency resolution is better, about 0.1 Hz

3. peak is about 0.75 Volt, less leakage but still strong

4. peak location is close, 9.96 Hz

Let’s get more points, keep same sampling frequency

fs = 25.0 #Hz
N = 512 # points
plotSignal(A,ff,fs,N)

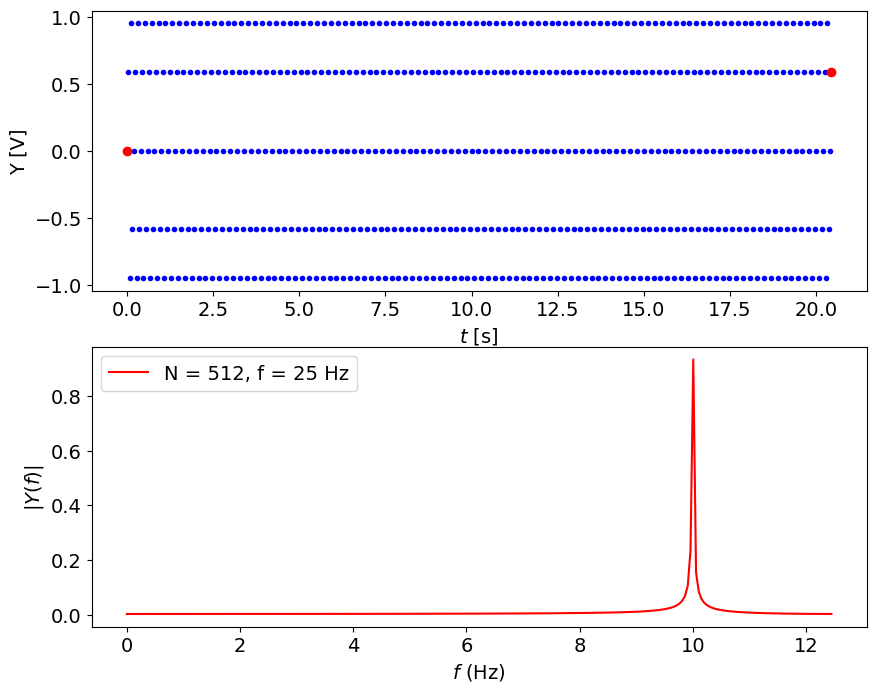
Note:

1. time sampling is much longer, \(T = N/f_s = 512/(25 Hz) = 20.48\) s

2. peak is narrow, at 10.01 Hz

3. resolution is good, much lower leakage, value is close to 0.9 Volt

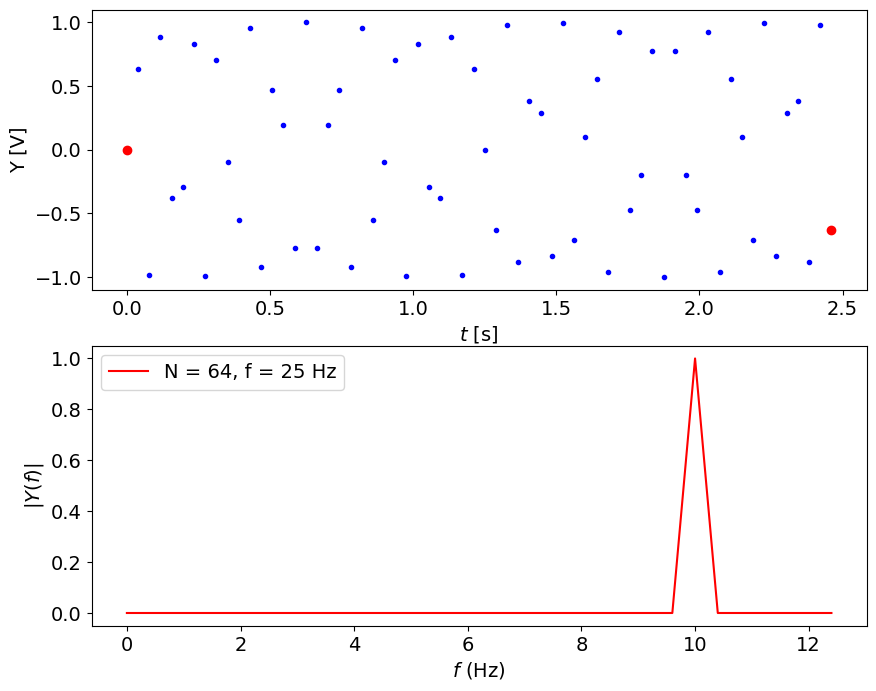
Still, how to get the perfect spectrum? Use tricks, for instance, sample at a specific frequency:

fs = 25.6 #Hz
N = 256 # points
plotSignal(A,ff,fs,N)

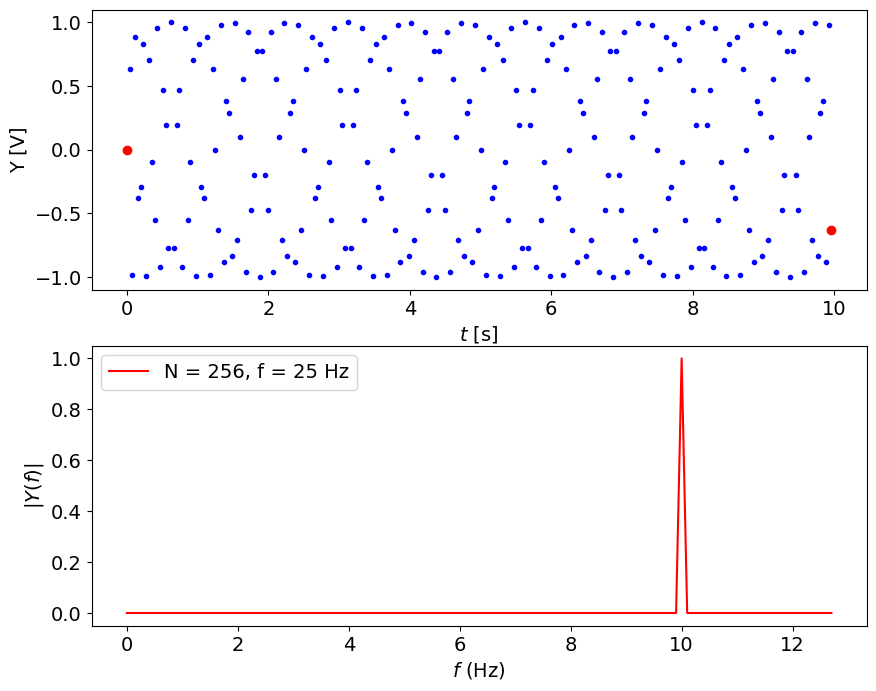
# After you know the real value, you can save a lot of time:
fs = 25.6 #Hz
N = 64 # points
plotSignal(A,ff,fs,N)