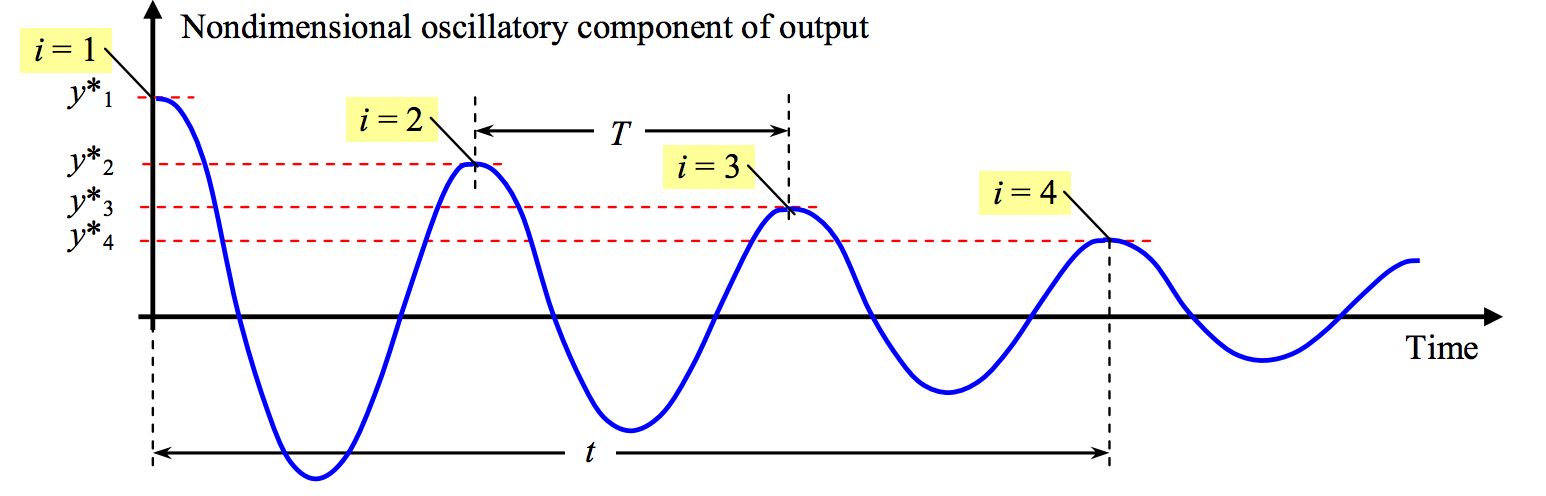
Log decrement method#
based on lectures of Prof. Cimbala, ME341
The log-decrement method#
The log-decrement is based on the following analysis: $\( \frac{q_o}{Kq_{is}} = 1-e^{-\zeta \omega_n t} \left[ \frac{1}{\sqrt{1-\zeta^2}}\sin\left(\omega_n t \sqrt{1-\zeta^2} + \sin^{-1} \left(\sqrt{1-\zeta^2} \right) \right) \right]\)$
and the damped natural frequency: $\(\omega_d = \omega_n \sqrt{1-\zeta^2}\)$
Using the output of the system in time (step function response) we need to solve for \(\omega_n\) and \(\zeta\) simultaneously. The practical solution is the log-decrement method.
When \(\zeta \sim 0.1\div 0.3\), then the sine function is approximately \(\pm 1\) and the magnitude only (peaks of the oscillating function) behave approximately as:
Therefore we plot the normalized step founction output minus 1, obtain a function that oscillates around zero, and try to extract the peaks. We can use only positive peaks and mark them as \(y^*_i, \quad i=1\dots n\) and their time instants, \(t^*\). From these values we can obtain:
The period of oscillations if we measure the time \(t\) of \(n\) cycles (e.g. \(n=3\) in our example), $\( T = t/n \)$
If we define the \(\log\) of the reduction of amplitude between each peak as \(\delta\): $\( \ln \left(\frac{y^*_i}{y^*_{i+n}}\right) = n\delta\)\(, then the damping factor is recovered as: \)\( \zeta = \frac{\delta}{\sqrt{(2\pi)^2+\delta^2}}\)\( and the rest is straightforward: \)\( \omega_d = \frac{2\pi}{T} = 2\pi f_d\)\( and \)\( \omega_n = 2\pi f_n = \frac{\omega_d}{\sqrt{1-\zeta^2}} \)$
%pylab inline
%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib
from scipy import signal
# Define transfer function
k = 1 # sensitivity
wn = 546.72 # rad/s
z=0.2 # damping
sys = signal.lti(k*wn**2,[1,2*z*wn, wn**2])
# step function output
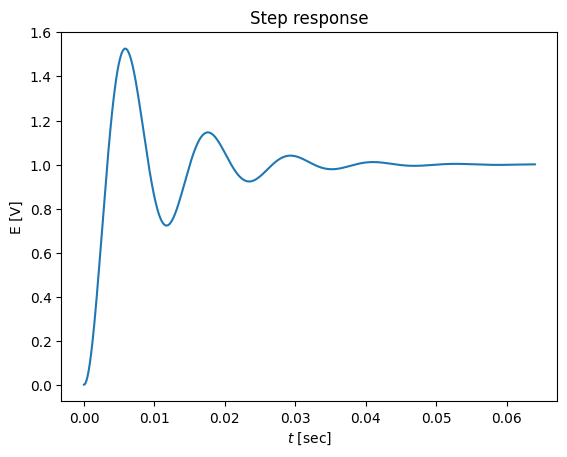
t,y = sys.step(N=1000)
plot(t,y)
title('Step response')
xlabel('$t$ [sec]')
ylabel('E [V]')
Text(0, 0.5, 'E [V]')
# note that sampling is sufficient, if not we need to apply the D/A reconstruction
# or interpolations, which will add more noise and uncertainty to the system identification
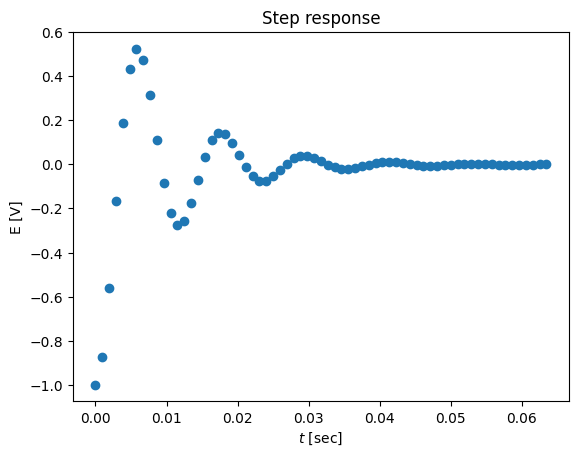
# plot the data as a decrement
ts = t[::15]
ys = y[::15]
plot(ts,ys-1,'o')
title('Step response')
xlabel('$t$ [sec]')
ylabel('E [V]')
Text(0, 0.5, 'E [V]')
# we will use the open source peakdetect function from
def peakdet(v, delta, x = None):
"""
Converted from MATLAB script at http://billauer.co.il/peakdet.html
Returns two arrays
function [maxtab, mintab]=peakdet(v, delta, x)
%PEAKDET Detect peaks in a vector
% [MAXTAB, MINTAB] = PEAKDET(V, DELTA) finds the local
% maxima and minima ("peaks") in the vector V.
% MAXTAB and MINTAB consists of two columns. Column 1
% contains indices in V, and column 2 the found values.
%
% With [MAXTAB, MINTAB] = PEAKDET(V, DELTA, X) the indices
% in MAXTAB and MINTAB are replaced with the corresponding
% X-values.
%
% A point is considered a maximum peak if it has the maximal
% value, and was preceded (to the left) by a value lower by
% DELTA.
% Eli Billauer, 3.4.05 (Explicitly not copyrighted).
% This function is released to the public domain; Any use is allowed.
"""
maxtab = []
mintab = []
if x is None:
x = arange(len(v))
v = asarray(v)
if len(v) != len(x):
sys.exit('Input vectors v and x must have same length')
if not isscalar(delta):
sys.exit('Input argument delta must be a scalar')
if delta <= 0:
sys.exit('Input argument delta must be positive')
mn, mx = Inf, -Inf
mnpos, mxpos = NaN, NaN
lookformax = True
for i in arange(len(v)):
this = v[i]
if this > mx:
mx = this
mxpos = x[i]
if this < mn:
mn = this
mnpos = x[i]
if lookformax:
if this < mx-delta:
maxtab.append((mxpos, mx))
mn = this
mnpos = x[i]
lookformax = False
else:
if this > mn+delta:
mintab.append((mnpos, mn))
mx = this
mxpos = x[i]
lookformax = True
return array(maxtab), array(mintab)
# if __name__=="__main__":
# from matplotlib.pyplot import plot, scatter, show
# series = [0,0,0,2,0,0,0,-2,0,0,0,2,0,0,0,-2,0]
# maxtab, mintab = peakdet(series,.3)
# plot(series)
# scatter(array(maxtab)[:,0], array(maxtab)[:,1], color='blue')
# scatter(array(mintab)[:,0], array(mintab)[:,1], color='red')
# show()
maxtab, mintab = peakdet(ys-1,.01,ts)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[7], line 1
----> 1 maxtab, mintab = peakdet(ys-1,.01,ts)
Cell In[6], line 45, in peakdet(v, delta, x)
42 if delta <= 0:
43 sys.exit('Input argument delta must be positive')
---> 45 mn, mx = Inf, -Inf
46 mnpos, mxpos = NaN, NaN
48 lookformax = True
NameError: name 'Inf' is not defined
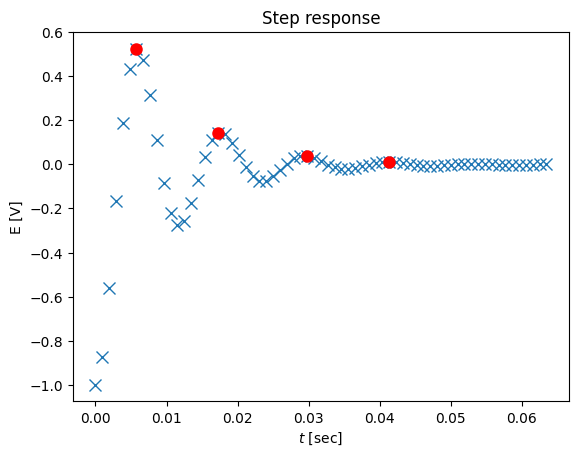
# we need only positive peaks, maxima:
maxtab
array([[0.0057674 , 0.52586962],
[0.0173022 , 0.14414951],
[0.02979824, 0.03919356],
[0.04133304, 0.01110418]])
# We see 4 peaks and therefore n = 4
tstar = maxtab[:,0]
ystar = maxtab[:,1]
# plot the data with the peaks
plot(ts,ys-1,'x',tstar,ystar,'ro',markersize=8)
title('Step response')
xlabel('$t$ [sec]')
ylabel('E [V]')
Text(0, 0.5, 'E [V]')
n = len(tstar)-1
print("cycles = %d" % n)
cycles = 3
T = (tstar[-1] - tstar[0])/(n)
print ("period T= %4.3f sec" % T)
period T= 0.012 sec
# delta
d = log(ystar[0]/ystar[-1])/(n)
print ("delta = %4.3f " % d)
delta = 1.286
# recover the damping and the frequency:
zeta= d/(sqrt((2*pi)**2 + d**2))
omegad = 2*pi/T
omegan = omegad/(sqrt(1-zeta**2))
# output
print ("natural frequency = %4.3f" % omegan)
print ("damping factor = %4.3f" % zeta)
print ("compare to the original: 546.72, 0.2")
natural frequency = 540.979
damping factor = 0.201
compare to the original: 546.72, 0.2