Calibration and uncertainty analysis - virtual experiment#
import numpy as np
import matplotlib.pyplot as pl
from scipy import stats
%matplotlib inline
pl.rcParams['figure.figsize'] = 10, 8
pl.rcParams['font.size'] = 18
from IPython.display import Image
Image('../img/pressure_calibration_table.png')

ptrue = 10.000
p = np.array([10.02, 10.20, 10.26, 10.20, 10.22, 10.13, 9.97, 10.12,
10.09, 9.9, 10.05, 10.17, 10.42, 10.21, 10.23, 10.11, 9.98, 10.10, 10.04, 9.81])
print(f'Pressure (Pa) {p}')
Pressure (Pa) [10.02 10.2 10.26 10.2 10.22 10.13 9.97 10.12 10.09 9.9 10.05 10.17
10.42 10.21 10.23 10.11 9.98 10.1 10.04 9.81]
Recommendations for choice of the histogram size:#
Let’s build histogram, we need to select the number of bins or \(\Delta p\)
\(k\) or number of bins shall be at least 5:
\(k \geq 5\)
There are several different methods to estimate the right number of bins for the histogram:
\(K = 1.87(N-1)^{0.4} + 1\)
or
\(K = N^{1/2}\)
histogram is defined as: \( Z = \frac{n(y)}{N \Delta y}\)
where \(\Delta y\) bin size, \(N\) total number of readings, \(n(y)\) is the number of readings in some bin, centered at \(y\)
K = 1.87*(p.size - 1)**(0.4);
print(f'Number of bins could be {K}')
K = np.sqrt(p.size);
print(f'Number of bins could be {K}')
K = 9
dp = (np.max(p) - np.min(p))/K;
print(f'Delta P = {dp}')
bins = np.r_[np.min(p)-dp:np.max(p)+dp:dp];
print(f'bins = {bins}') # row vector
Number of bins could be 6.0721577674237
Number of bins could be 4.47213595499958
Delta P = 0.06777777777777771
bins = [ 9.74222222 9.81 9.87777778 9.94555556 10.01333333 10.08111111
10.14888889 10.21666667 10.28444444 10.35222222 10.42 ]
hist, bin_edges = np.histogram(p,bins=bins)
hist
array([0, 1, 1, 2, 3, 5, 4, 3, 0, 1])
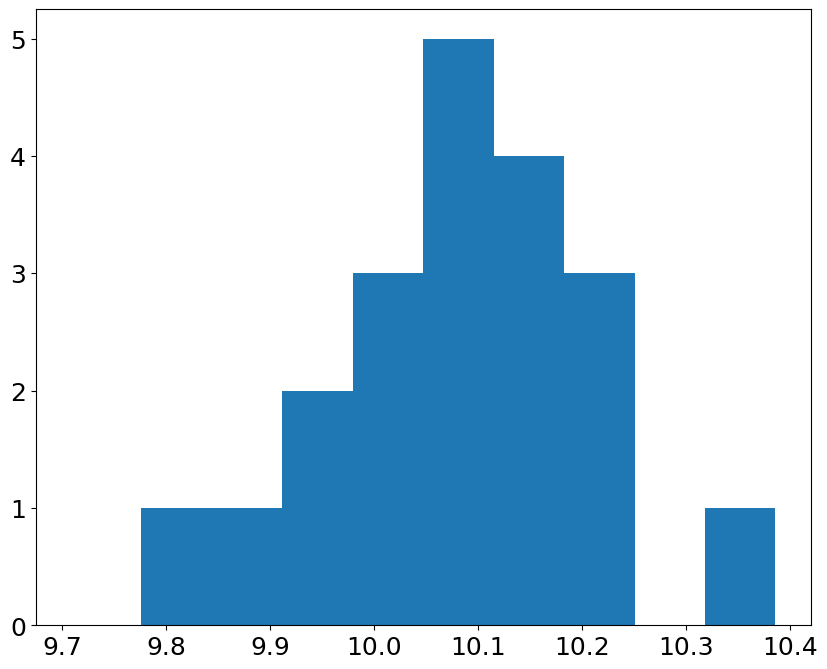
pl.bar(bin_edges[:-1], hist, dp)
<BarContainer object of 10 artists>
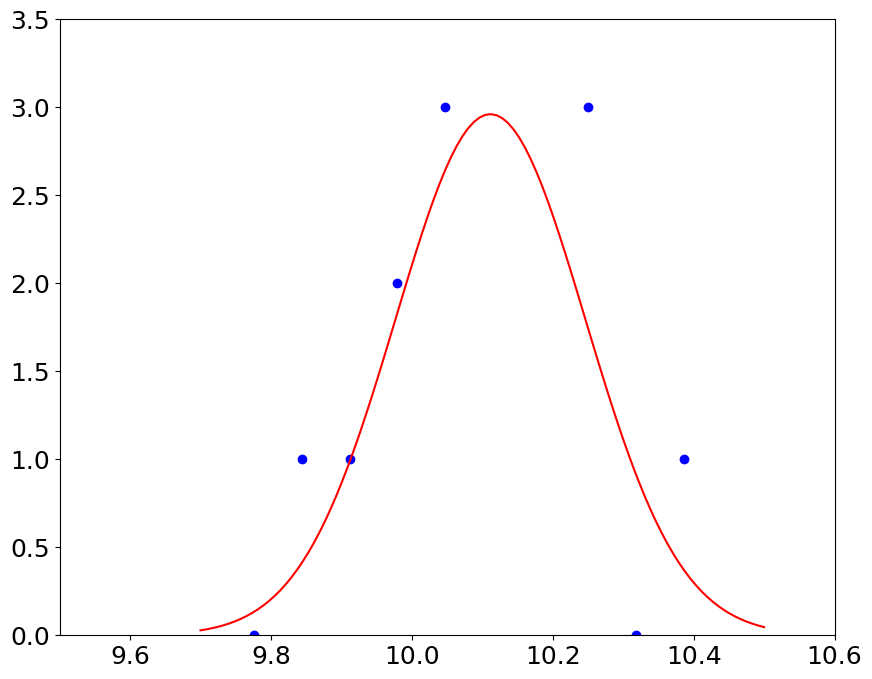
we expect to see the Gaussian, if our pressure measurements contain random errors#
mu = np.mean(p)
sigma = np.std(p)
print('mean, std %3.2f, %3.2f' % (mu, sigma))
x = np.linspace(9.7,10.5,100)
gauss = 1./np.sqrt(2*np.pi*sigma**2)*np.exp(-((x-mu)**2/(2*sigma**2)))
mean, std 10.11, 0.13
pl.plot(bin_edges[:-1]+dp/2,hist,'bo',x,gauss,'r')
pl.ylim(0,3.5)
pl.xlim(9.5, 10.6)
(9.5, 10.6)
\(\chi^2\) test#
How do we check if our histogram is similar to the Gaussian (or any other) distribution? Goodness-of-fit is called the \(\chi^2\) test
\(\chi^2 = \sum\limits_{i=1}^{n} \frac{(measured_i - expected_i)^2}{expected_i} \)
gauss = 1./np.sqrt(2*np.pi*sigma**2)*np.exp(-((bin_edges[:-1]+dp/2.-mu)**2/(2*sigma**2)))
chisq = np.sum((hist - gauss)**2/gauss)
print('$\chi^2$ = %f' % chisq)
$\chi^2$ = 6.126602
# degrees of freedom = number of bins minus the (order of the fit + 1):
print ('Number of degrees of freedom, K - (m+1) = %d' % (K - 2))
Number of degrees of freedom, K - (m+1) = 7
from scipy import stats
pval = 1 - stats.chi2.cdf(chisq, K-2);
print ('Confidence level is %3.1f percent' % (pval*100) )
Image('../img/chi_square_graph.png')
Confidence level is 52.5 percent
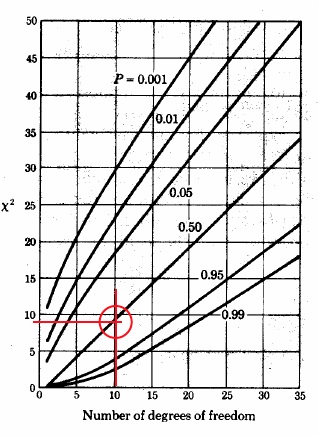
we conclude that for the given set of measurements we are only 50% certain that we can use the Gaussian distribution assumptions#
Calibration#
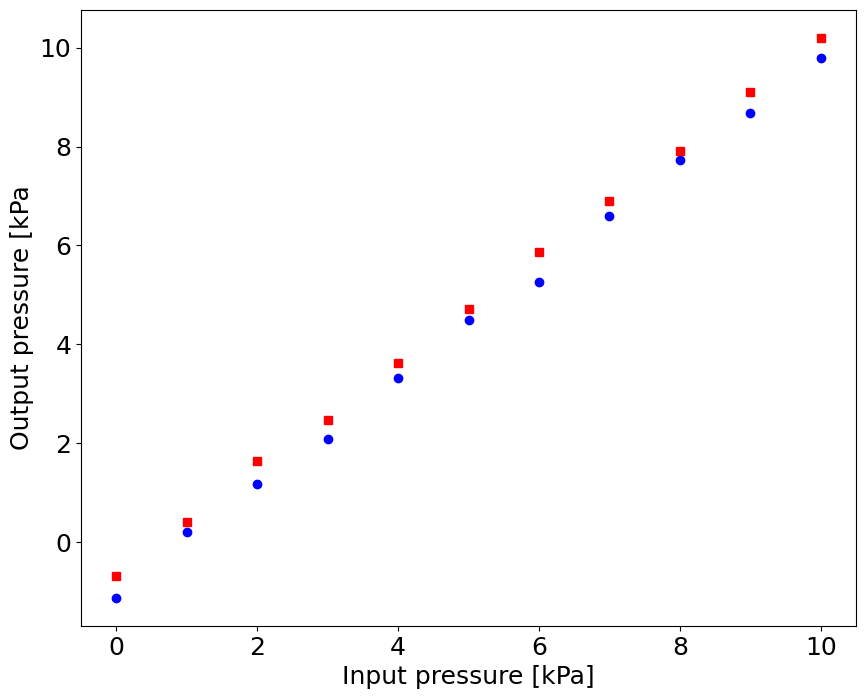
# Increasing pressure:
p_in_up = np.linspace(0.0,10.0,11)
p_out_up = np.array([-1.12, 0.21, 1.18, 2.09, 3.33, 4.50, 5.26, 6.59, 7.73, 8.68, 9.8])
# Decreasing pressure
p_in_down = np.flipud(p_in_up)
p_out_down = np.array([10.20, 9.10, 7.92, 6.89, 5.87, 4.71, 3.62, 2.48, 1.65, 0.42, -0.69])
pl.plot(p_in_up,p_out_up,'bo',p_in_down,p_out_down,'rs')
pl.xlabel('Input pressure [kPa]')
pl.ylabel('Output pressure [kPa')
Text(0, 0.5, 'Output pressure [kPa')
x = np.r_[p_in_up,p_in_down]
y = np.r_[p_out_up,p_out_down]
np.polyfit(x,y,1)
array([ 1.08231818, -0.84704545])
Estimate uncertainty#
\(q_0 = m q_i + b\)
\(q_0 = 1.08 q_i + 0.85\)
\(\sigma_{q_0}^2 = \frac{1}{N} \sum (m q_i + b - q_0)\)
We then use the inverse of the calibration curve to get the inputs from the outputs:
\(q_i = \frac{q_0 - b}{m}\)
\(\sigma_{q_i}^2 = \frac{1}{N} \sum \left( \frac{q_0 - b}{m} - q_i \right)^2 = \frac{\sigma_{q_0}^2}{m^2} \)
m = 1.08
b = -0.85
std_q0 = np.sqrt(1./(y.size-1) * np.sum((m*x + b - y)**2))
print ('std(q_0) = %f ' % std_q0)
std(q_0) = 0.203727
# let's assume we measured output
q_0 = 4.32 #kPa
# we estimate the real input as:
q_i = (q_0 - b)/m
# and its std. dev.
std_qi = std_q0/m
print ('q_i = %3.2f +- %3.2f kPa ' % (q_i, 3*std_qi))
q_i = 4.79 +- 0.57 kPa
# we can visualize the result as:
# Image('../img/result_pressure_measurement.png')
Uncertainties of least-square best fit estimates:#
\(S_y^2 = \frac{1}{N-1} \sum\limits_{i=1}^N (y_i - \overline{y})^2 \)
\(S_{yx}^2 = \frac{1}{\nu} \sum\limits_{i=1}^N (y_i - \overline{y_{c_i}})^2\)
\(\nu = N - (m+1)\)
\(S_m = S_{yx}^2 \frac{N}{N\sum\limits_{i=1}^N x_i^2 - \left( \sum\limits_{i=1}^N x_i \right)^2} \)
\(S_b = S_{yx}^2 \frac{N\sum\limits_{i=1}^N x_i^2}{N \left[N\sum\limits_{i=1}^N x_i^2 - \left( \sum\limits_{i=1}^N x_i \right)^2 \right]} \)
\(S_m = 0.0134\) - sensitivity uncertainty
\(S_b = 0.078\) - zero shift uncertainty
\( m = 1.08 \pm 0.04\)
\( b = -0.85 \pm 0.24 \) kPa