Using simulations to explain uncertainty#
From the blog of engineering.com
Why Simulation is the Future of Uncertainty Evaluation#
Introduction#
The conventional method for calculating uncertainty has significant limitations:
Only exact for measurements represented by simple linear equations
Only works when input uncertainties are normally distributed
Complex measurements lead to errors in uncertainty combination
This guide explains why simulation methods offer superior uncertainty evaluation.
Simple Linear Models#
Let’s start with the simplest case: two influences adding to give a measurement result.
For this linear combination:
Increasing a by one unit increases y by one unit
Independent of value of b
All sensitivity coefficients equal one
The law of propagation of uncertainty gives:
Distribution Effects#
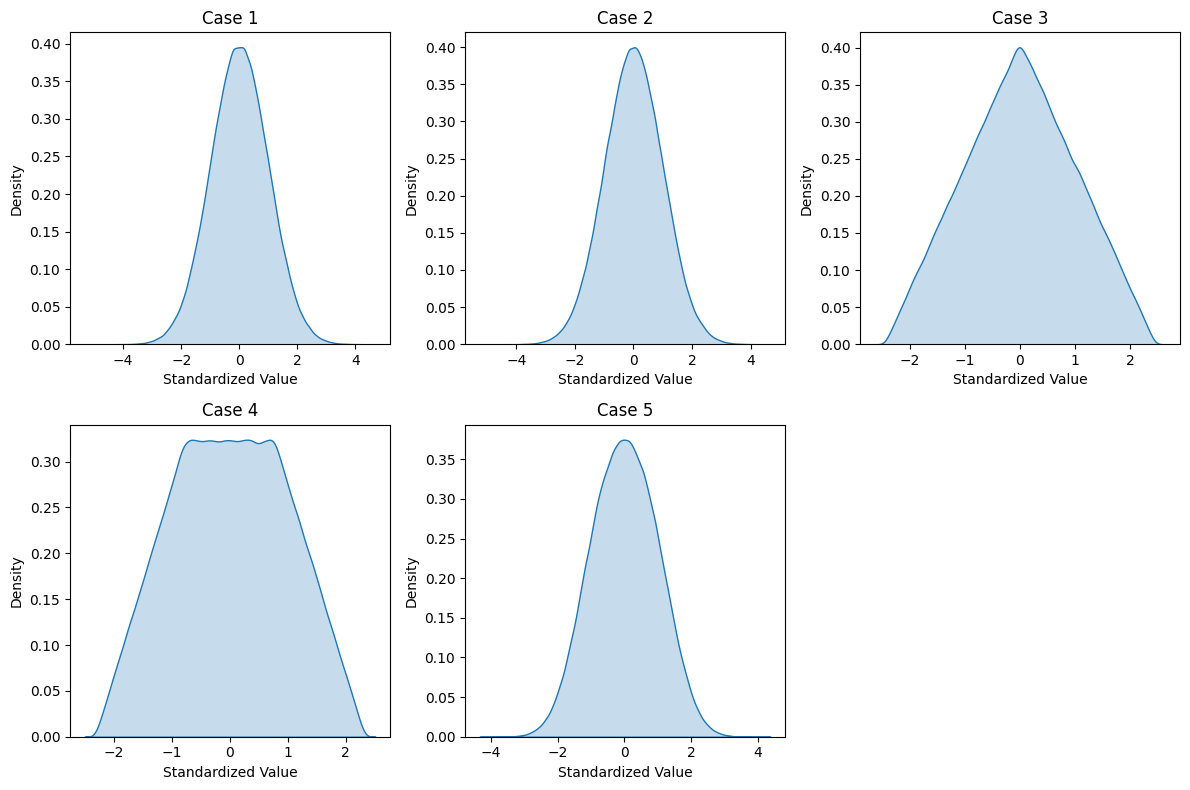
Even in this simple case, output distributions vary:
Two normal distributions:
Output is normal if inputs have similar size
Output deviates from normal if inputs differ significantly
Two uniform distributions:
Output is triangular if inputs have same size
Output is complex if inputs differ in size
Mixed distributions:
Combining normal and uniform gives complex distributions
Hard to predict without simulation
How Simulation Works#
Basic steps in measurement simulation:
Define measurement function:
where x is a vector of influence quantities
Generate random values:
Create vector r of m random draws
Use appropriate probability distributions
Scale by uncertainty values
Matrix formulation:
where:
X is m × n matrix of simulated values
x₀ is vector of nominal values
u is uncertainties
r is random draws
Calculate results:
Find confidence intervals:
where p is proportion counted from each end
Non-linear Measurements#
Example 1: Thermal Expansion#
Measurement model:
First-order uncertainty approximation:
Third-order approximation adds terms:
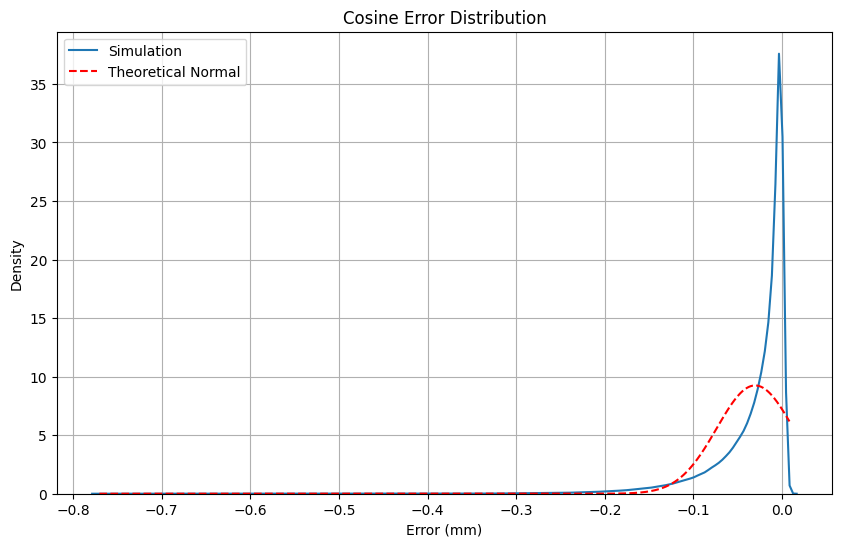
Example 2: Cosine Error#
For a 200mm length measurement:
Length uncertainty: 2 μm
Alignment uncertainty: 1 degree
Results show:
Non-normal distribution
Significant differences between theory and simulation
Larger differences at higher confidence levels
Comparison of Methods#
Standard Uncertainty#
Similar results between theory and simulation
First-order approximation often sufficient
95% Confidence Level#
Different confidence limit positions
Similar total uncertainty range
99.9% Confidence Level#
Total range almost doubles
Upper bound 3.5× theoretical prediction
Differences increase with confidence level
Best Practices for Simulation#
Number of Trials
Use minimum of 1 million trials
More trials for higher confidence levels
Check convergence by increasing trials
Distribution Selection
Match actual measurement conditions
Consider all uncertainty sources
Document assumptions
Validation
Compare with analytical methods when possible
Check sensitivity to input parameters
Verify numerical stability
Documentation
Record all simulation parameters
Specify distributions used
State confidence levels
Advantages of Simulation#
No Distribution Assumptions
Works with any input distribution
Handles non-normal outputs
Better for high confidence levels
Non-linear Functions
No approximation needed
Captures all-order effects
More reliable for complex measurements
Practical Benefits
Easier to implement
More intuitive understanding
Better handling of asymmetric distributions
When to Use Simulation#
Always for:
High confidence levels (>95%)
Non-linear measurements
Mixed distributions
Complex measurement models
Consider for:
Quality-critical measurements
Safety-related calculations
Regulatory compliance
Maybe not for:
Simple linear measurements
Normal distributions only
Low confidence levels
Quick approximations
Limitations and Considerations#
Computational Resources
Large number of trials needed
May require significant processing time
Storage for large datasets
Expertise Required
Understanding of statistics
Programming knowledge
Validation methods
Validation
Check convergence
Verify input distributions
Compare with analytical methods
Conclusion#
Simulation offers significant advantages over traditional analytical methods for uncertainty evaluation:
More accurate for complex measurements
Better handling of different distributions
More reliable at high confidence levels
Future of uncertainty evaluation in quality engineering
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import seaborn as sns
%matplotlib inline
def simulate_linear_combination(n_trials=1_000_000, case=1):
"""
Simulates different cases of combining uncertainties
case 1: 2 normal distributions of similar size
case 2: 2 normal distributions of different sizes
case 3: 2 uniform distributions of same size
case 4: 2 uniform distributions of different sizes
case 5: normal and uniform distribution
"""
np.random.seed(42) # for reproducibility
if case == 1:
a = np.random.normal(0, 1, n_trials)
b = np.random.normal(0, 1, n_trials)
elif case == 2:
a = np.random.normal(0, 1, n_trials)
b = np.random.normal(0, 2, n_trials)
elif case == 3:
a = np.random.uniform(-np.sqrt(3), np.sqrt(3), n_trials)
b = np.random.uniform(-np.sqrt(3), np.sqrt(3), n_trials)
elif case == 4:
a = np.random.uniform(-np.sqrt(3), np.sqrt(3), n_trials)
b = np.random.uniform(-2*np.sqrt(3), 2*np.sqrt(3), n_trials)
elif case == 5:
a = np.random.normal(0, 1, n_trials)
b = np.random.uniform(-np.sqrt(3), np.sqrt(3), n_trials)
y = a + b
return y
def plot_distributions():
"""Recreates Figure 1 from the paper"""
plt.figure(figsize=(12, 8))
cases = range(1, 6)
for i, case in enumerate(cases, 1):
y = simulate_linear_combination(case=i)
# Normalize the data
y = (y - np.mean(y)) / np.std(y)
plt.subplot(2, 3, i)
sns.kdeplot(y, fill=True)
plt.title(f'Case {i}')
plt.xlabel('Standardized Value')
plt.ylabel('Density')
plt.tight_layout()
plt.show()
def thermal_expansion_simulation(n_trials=1_000_000):
"""
Simulates thermal expansion measurement
dL = L * dT * a
"""
# Nominal values
L = 1.0 # m
dT = 2.3 # K
a = 23e-6 # m/m/K
# Uncertainties (5mm, 1K, 10%)
u_L = 0.005
u_dT = 1.0
u_a = 0.1 * a
# Generate random values
L_sim = np.random.normal(L, u_L, n_trials)
dT_sim = np.random.normal(dT, u_dT, n_trials)
a_sim = np.random.normal(a, u_a, n_trials)
# Calculate result
dL = L_sim * dT_sim * a_sim
return dL
def cosine_error_simulation(n_trials=1_000_000):
"""
Simulates length measurement with cosine error
L_measured = L_true * cos(theta)
"""
# Nominal values and uncertainties
L_true = 200 # mm
u_L = 0.002 # mm
u_theta = 1 # degree
# Generate random values
L_sim = np.random.normal(L_true, u_L, n_trials)
theta_sim = np.random.normal(0, u_theta, n_trials)
# Convert degrees to radians for calculation
theta_sim_rad = np.deg2rad(theta_sim)
# Calculate measured length with cosine error
L_measured = L_sim * np.cos(theta_sim_rad)
return L_measured - L_true # Return the error
def calculate_uncertainties(data, confidence_levels=[0.683, 0.954, 0.997]):
"""Calculate standard and expanded uncertainties"""
results = {}
# Standard uncertainty
results['std'] = np.std(data)
# Expanded uncertainties
for p in confidence_levels:
lower = (1-p)/2
upper = 1 - lower
results[f'{p:.1%}'] = {
'lower': np.quantile(data, lower),
'upper': np.quantile(data, upper)
}
return results
def compare_distributions():
"""Recreates Figure 4 from the paper"""
errors = cosine_error_simulation()
plt.figure(figsize=(10, 6))
# Plot simulation results
sns.kdeplot(errors, label='Simulation')
# Plot theoretical normal distribution
x = np.linspace(min(errors), max(errors), 1000)
plt.plot(x, stats.norm.pdf(x, np.mean(errors), np.std(errors)),
'r--', label='Theoretical Normal')
plt.title('Cosine Error Distribution')
plt.xlabel('Error (mm)')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.show()
def print_uncertainty_comparison():
"""Prints uncertainty comparison table"""
errors = cosine_error_simulation()
uncertainties = calculate_uncertainties(errors)
print("\nUncertainty Comparison:")
print(f"Standard Uncertainty: {uncertainties['std']:.6f} mm")
for level, values in uncertainties.items():
if isinstance(values, dict):
print(f"\n{level} Confidence Interval:")
print(f"Lower: {values['lower']:.6f} mm")
print(f"Upper: {values['upper']:.6f} mm")
if __name__ == "__main__":
# Generate all figures and results
print("Generating plots and results...")
# Figure 1: Distribution comparisons
plot_distributions()
# Thermal expansion simulation
dL = thermal_expansion_simulation()
print("\nThermal Expansion Results:")
print(f"Standard Uncertainty: {np.std(dL):.6f} m")
# Cosine error distribution and uncertainties
compare_distributions()
print_uncertainty_comparison()
Generating plots and results...
Thermal Expansion Results:
Standard Uncertainty: 0.000024 m
Uncertainty Comparison:
Standard Uncertainty: 0.043083 mm
68.3% Confidence Interval:
Lower: -0.060521 mm
Upper: -0.001550 mm
95.4% Confidence Interval:
Lower: -0.157121 mm
Upper: 0.001902 mm
99.7% Confidence Interval:
Lower: -0.308503 mm
Upper: 0.004422 mm
