Outliers

Outliers#

import numpy as np
import matplotlib.pyplot as pl
%matplotlib inline

import matplotlib as mpl
mpl.rcParams['lines.linewidth']=2
mpl.rcParams['lines.color']='r'
mpl.rcParams['figure.figsize']=(10,8)
mpl.rcParams['font.size']=14
mpl.rcParams['axes.labelsize']=20

Single variable, \(x\)#

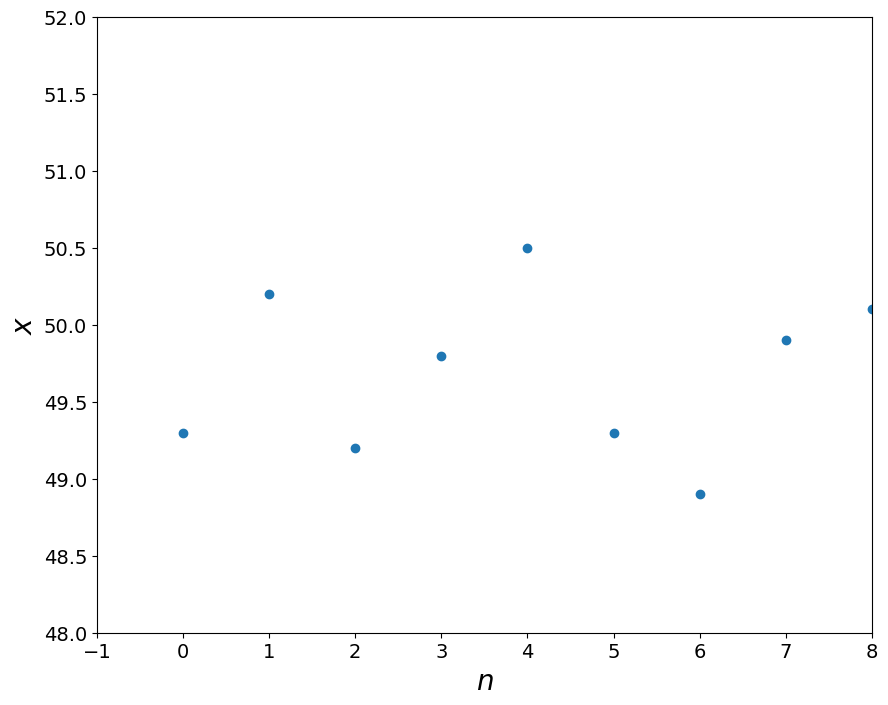
x = np.array([49.3,50.2,49.2,49.8,50.5,49.3,48.9,49.9,50.1,49.2])

pl.figure()
pl.plot(x,'o')
pl.xlim([-1,8])
pl.ylim([48,52])
pl.ylabel('$x$')
pl.xlabel('$n$')

Text(0.5, 0, '$n$')
../_images/d61793e508ab9b158ab7d7daab690fade099718d87b840a89d85675c4a3e4665.png

We use modified Thompson test (based on Student’s t-distribution)#

Sort the values#

x.sort()

x

array([48.9, 49.2, 49.2, 49.3, 49.3, 49.8, 49.9, 50.1, 50.2, 50.5])

pl.plot(x,'o')
pl.xlim([-1,8])
pl.ylim([48,52])
pl.ylabel('$x$')
pl.xlabel('$n$')

Text(0.5, 0, '$n$')
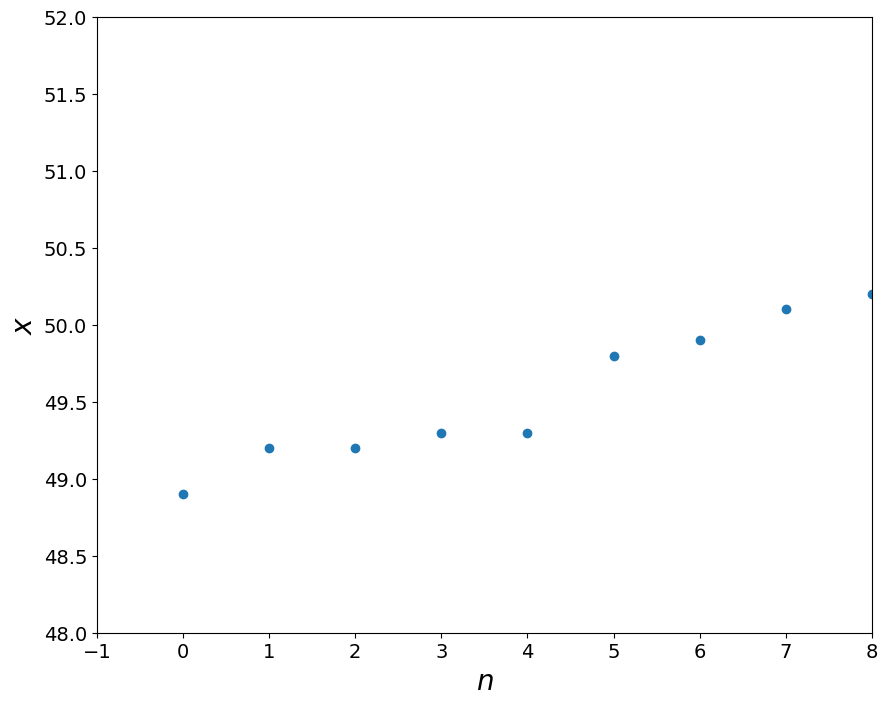
../_images/61808cc15ab5d2215d544f158a3afb766680aafe4e51311cec513e8e83273f43.png

Note: we suspect in the sorted list of values the first and the last

get the sample mean and sample standard deviation, get deviations#

x_mean = np.mean(x)
x_std = np.std(x,ddof=1)
print( x_mean)
print (x_std)

49.64
0.5295700562196137

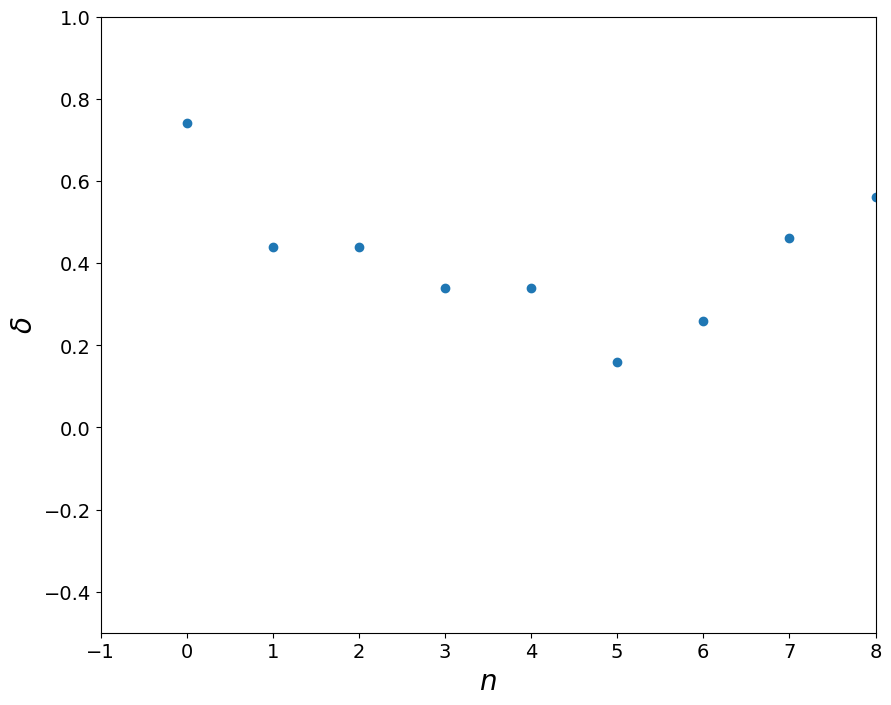
\(\delta_i = | x - x_i |\)

delta = abs(x - x_mean)
pl.plot(delta,'o')
pl.xlim([-1,8])
pl.ylim([-.5,1])
pl.ylabel('$\delta$')
pl.xlabel('$n$')
print (delta[0],delta[-1])

0.740000000000002 0.8599999999999994

<>:5: SyntaxWarning: invalid escape sequence '\d'
<>:5: SyntaxWarning: invalid escape sequence '\d'
/tmp/ipykernel_276332/2879644948.py:5: SyntaxWarning: invalid escape sequence '\d'
  pl.ylabel('$\delta$')
../_images/31b0cb95aafd026eafcb85ff50686dac650e606dd49d8a5bddeb190048f07fb0.png
Contents